|
Présentation
de quelques instruments
Arpentage
et nivellement antiques
applications
à des opérations simples
Sommaire
(A
l'intention du personnel éducatif
du Site du pont du Gard)
Lundi
14 février 2005
par Claude Larnac
Ce
travail a été présenté au
personnel éducatif du site du pont du Gard
afin de lui apporter quelques éléments de réflexion sur des questions
souvent posées, relatives à la détermination des pentes (dénivelées), à
l’orientation, aux relevés topographiques, aux calculs de hauteurs, de
distance, etc.
Les bases de ce document se trouvent en particulier dans
:
1.
les Actes du Colloque international sur le thème de la Dioptre d’Héron
d’Alexandrie qui s’est tenu les 17,
18 et 19 juin 1999, au Centre Jean Palerne, Université de Saint-Etienne
(Loire).
2. L’arpentage romain de Gérard
Chouquer et François Favory avec la collaboration d’Anne Roth-Congès - Ed.
Errance – 2001.
3.
Réflexions
sur l’aqueduc romain de Nîmes –
Claude Larnac – En cours d’édition : CDDP de Nîmes.
Cette
journée de formation consistait, le matin, en une présentation théorique,
accompagnée d’exercices pratiques simples sur place, et l’après-midi en
une application sur le terrain : hauteur des niveaux 2 et 2-3 du pont du
Gard, largeur du Gardon au droit de la rivière.

Quelques
notes sur les auteurs antiques cités dans le texte
————
Frontin
-
Curateur des eaux
des aqueducs de Rome (97-98 ap. J.-C. jusqu’à sa mort 103-104 ?),
Frontin aurait écrit des textes sur la gromatique (limitations,
arpentage) avant l’an 98.
Hygin - Lequel ? G. Chouquer et F.
Favory en mentionnent trois
-
Hygin
« tout court » est un arpenteur, auteur de trois traités (II e
siècle ap. J.-C.)
-
Hygin
(le) gromatique, souvent cité
-
Pseudo-Hygin,
un auteur anonyme qu’on nomme ainsi, mais parfois encore le gromatique.
D’où les incertitudes inhérentes aux confusions apportées par les noms.
Il était spécialiste de l’arpentage des camps militaires.
Balbus - Arpenteur
(II e siècle ap. J.-C.)
Iunius Nypsius (ou
Nypsus ou Nipsus) - cité de nombreuses fois par Anne Roth-Congès (Colloque de
St-Etienne).
Pythagore - (572 ?- 493 av.
J.-C.)- remarquable mathématicien auquel on attribue la très célèbre propriété
qui régit la relation entre les trois côtés d’un triangle rectangle. Nous réservons
une page à ladite propriété, pressentie par les Babyloniens quinze siècle siècles
avant sa naissance et démontrée deux siècles plus tard par Euclide.
EUCLIDE
- (365 ?
– 276 av. J.-C.). Son œuvre
est immense tant par la diversité des sujets que par la qualité de son
travail. Il démontra le théorème « de Pythagore ».
Il établit les lois de la réflexion de la lumière que nous utiliserons
dans nos exercices pratiques, lois
attribuées 19 siècles plus tard à Descartes…
Nous
ne citons que deux de ses œuvres parce que nous les évoquons au moins une fois
dans ce texte : les treize livres sur les Eléments (géométrie
plane, géométrie dans l’espace, arithmétique) et un traité d’optique.
VERUS
- le
boutiquier de Pompéi qui, lors de l’éruption du Vésuve (79 ap. J.-C.), détenait
une groma et divers autres instruments de nivellement.
Vitruve - (88-26 av.
J.-C.), ingénieur-architecte qui vécut à l’époque
de César, nous intéresse par le livre VIII de De Architectura , qui
traite de l’eau : repérage des sources, captage, conduite de l’eau,
distribution dans les villes. Mais « on ne saurait dire avec certitude si
le livre VIII du De Architectura, est le fruit d’une expérience
professionnelle ou, au contraire, si l’activité de Vitruve à
l’administration des eaux consacra la notoriété d’un livre qui touchait à
ces problèmes » (Louis Callebat, professeur à l’Université de Caen,
traducteur du livre VIII). Vitruve commit entre autres, et par manque de précision,
des erreurs sur les conditions d’écoulement des eaux dans un canal ou sur les
caractéristiques du chorobate.
HÉRON
D’ALEXANDRIE - (I er siècle ap. J.-C.,
selon Dimitris Raïos), auteur du traité de La Dioptre, au travers
duquel il aborde aussi bien la géométrie
pure, la topographie, la technique des mesures, l’hydrographie, la mécanique
des fluides, etc. Sa dioptre, ancêtre de l’actuel théodolite, dans laquelle
les réglages se faisaient par des niveaux à eau et des fils à plomb, trouvait
son utilité en topographie, sur terrain plat ou accidenté, pour mesurer les
hauteurs inaccessibles, repérer les prolongements des tracés souterrains ou en
astronomie.

Les
auteurs modernes cités pendant la journée
(ouvrages ou communications)
———
I - Gérard Chouquer et François Favory -
L’arpentage romain – Ed. Errance -
2001.
II - In
Argoud-Guillaumin -
Colloque international de Saint-Etienne Autour de la Dioptre d’Héron
d’Alexandrie -
2000 - Publications de l’Université
de Saint-Etienne :
-
André
ALLard -
Université catholique de Louvain -
La formule héronienne de
l’aire d’un triangle scalène
-
Gilbert
Argoud
- Université
Jean Monnet – Saint-Etienne -
Utilisation de la
dioptre en hudraulique
-
Jean
Burdy, Agrégé de l’Université,
Lyon –
Les aqueducs de Lugdunum (91-106)
-
Monique Clavel-Lévèque,
- Université de Franche-Comté, Besançon
Groma
et pratiques d’aménagement
du territoire en Biterrois
-
Gisèle Coco –
université de Provence, Aix-en_Provence -
Un dossier : la dioptre à travers les traités
de l’astrolabe plan
-
Micheline
Decorps-Foulquier -
Université de Caen -
Remarques liminaires
sur le texte de la dioptre de Héron d’Alexandrie et ses sources
-
Joëlle Delattre -
Université de Lille -
Théon de Smyrne et la Dioptre
-
Marie
Feyel - Ecole
française d’Athènes -
Comment restituer
la dioptre d’héron d’Alexandrie?
-
Philippe Fleury-
Université de Caen -
L’odomètre d’Héron d’Alexandrie
-
Dr.-Ing - Klaus
Grewe -
Landschaftsverband Rheinland, Bonn -
Le tracement d’un tunnel dans l’Antiquité : la théorie
et la pratique
-
Jean-Claude
Guillaumin
- Université de Franche-Comté, Besançon
-
La première partie du chapitre 25 de la Dioptre :
avatars d’une figure et d’un texte
-
Alain
Hairie – CNRS –
Laboratoire d’études et de recherches sur les matériaux (LERMAT), Caen -
Aspects pratiques de la dioptre d’Héron d’Alexandrie, étude
théorique et expérimentale de la précision des mesures réalisables
-
Catherine
Jacquemard - Université de
Caen -
La mesure d’une hauteur dont le pied est inaccessible. Etude de Héron
-
Claude Larnac - Professeur de
mathématiques retraité, Pt honoraire du CIDS, Castillon-du-Gard
Les limites du système
œil-chorobate relativement à l’implantation
de l’aqueduc de Nîmes
-
Georges
Marchand, Géomètre
topographe, UMR 154 du CNRS (Lattes - Montpellier),
Hervé Petitot - AFAN
- Méditerranée - et Laurent
Vidal, UMR 6048 du CNRS,
Besançon -
L’équerre d’arpenteur de l’Orme à Ennemain (Somme)
-
Dimitris
Raios
– Université de Ioannina (Grèce) -
La date d’Héron d’Alexandrie –témoignages internes et cadre
historico-culture
-
Anne
Roth-Congés – CNRS, UMR
154 du CNRS (Lattes-Montpellier)-
Questions d’arpentage dans
la Dioptre et les textes gromatiques romains
-
Pierre
Souffrin, astrophysicien à
l’observatoire de Nice,
Remarques sur la datation de la Dioptre d’Héron d’Alexandrie par l’éclipse
de lune de 62.
Limitation
et Arpentage
———
Arpentage
« L’arpentage courant, de
tradition immémoriale, concerne toutes les opérations de topographie, levées
de terrain à usage cadastral, architectural ou urbanistique » (G.
Chouquer F. Favory)
Le mensor ou
limitator (terme anachronique), le géomètre topographe, est le
personnage clé de la limitation. Il sait lever un plan, calculer les aires
d’un terrain ou d’un territoire aux contours irréguliers.
Limitation
« La
limitation au contraire s’inscrit dans le temps : c’est un système original
de découpage du sol régulièrement corroyé par des chemins (limites en
latin), étendu au territoire de la colonie ou de toute autre cité de statut
variable dans toutes les provinces de l’Empire » (id°).
Formule d’Héron, pour le
calcul de l’aire d’un triangle en fonction de ses trois côtés.
Où a, b,
c sont les mesures des côtés et p le demi-périmètre. Malgré sa complexité
apparente, cette formule, qu’on enseigne toujours aux élèves des classes de
premières scientifiques, est d’un emploi très pratique puisqu’elle ne nécessite
pas de calcul de hauteur.
Par exemple si un triangle ABC a pour côtés :
BC
qu’on note a = 8
AC
qu’on note c = 10
AB
qu’on note c = 12, le périmètre 2p
= 8 + 10 = 12 = 30 ;
et :
p
= 15,
p - a
= 15 - 8 = 7
p - b
= 15 - 10 = 5
p - c
= 15 – 12 = 3
S = √15 x 7 x 5 x 3 =
√1575 ,
voisin de √1600,
c’est-à-dire 40 (plus précisément 39,69).
On peut décomposer tout polygone en
triangles et répéter cette formule autant de fois que nécessaire. Les aires
des parties informes extérieures, stériles,
(subsecivum : subsécive) peuvent s’évaluer par des méthodes
d’approximation.
Limitation ou arpentage sont des opérations différentes
qui utilisent les mêmes instruments.
L’activité que nous menons dans le cadre de cette journée est du domaine
de l’arpentage et du nivellement.

Quelques
notes sur la propriété de Pythagore
———
Bien
avant Pythagore, les Babyloniens ….
Sur la tablette YBC 7289, d’environ
16 cm², le scribe a gravé un carré avec ses diagonales. Le long d’un côté,
le nombre 30, au-dessus d’une diagonale, le nombre 1,414
en notation sexagésimale. Et au-dessous de cette même diagonale,
toujours dans cette notation, 42,41, lequel est le produit de 30 par 1,414. Ce
résultat est exactement conforme à la règle selon laquelle la diagonale
d’un carré est égale au produit de la mesure du côté par √2.
Ainsi, vers 1700 à 1900 av. J.-C., les Babyloniens connaissaient un cas
particulier de la réciproque du théorème de Pythagore. Ils savaient aussi
qu’un triangle dont les côtés ont pour mesure 3,4,5 est rectangle et
que le carré du plus grand côté est égal
à la somme des carrés des deux autres : 5² = 3² + 4²
ou 25 = 9 + 16
…
Treize siècles plus tard vint
Pythagore
Cette propriété, toujours non démontrée, fort intéressante, est
attribuée à Pythagore. Henri, en 1615 commente
la cérémonie : lequel (Pythagore) en fut si content et joyeux,
que pour en rendre grâce aux dieux, plusieurs disent qu’il sacrifia une Hécatombe
(sacrifice de cent boeufs) et d’autres
rapportent qu’il ne leur sacrifia qu’un bœuf ; ce qui est plus
vray-semblable que non pas qu’il en ait immolé cent, veu que ce philosophe
faisoit très grand scrupule d’espandre
le sang des animaux ».
Et
enfin Euclide en donna la démonstration (livre 1, proposition 47)
« Aux triangles rectangles, le quarré du costé qui soustient
l’angle droict, est égal aux quarrez des deux autres costez »
(Traduction de Henrion, 1615).
Les applications furent surtout orientées vers le tracé d’un angle
droit. Nous retiendrons en particulier la construction des perpendiculaires
à l’aide de la corde à 13 nœuds.

L’équipement
des arpenteurs
———
Le
gnomon
L’orientation d’une carte, repose
sur le repérage des points cardinaux.
Chercher
l’orient ?
Comment le repérer? Le soleil ne se lève que deux fois par an à l’Est
(l’orient)
Alors …. on cherche le Nord.
Le jour : en mettant en évidence la direction du sud à midi
locale (gnomon)
La nuit :
en repérant l’étoile polaire (située actuellement à moins d’un degré du
pôle nord géographique).
Le
gnomon :
C’est un bâton planté verticalement dans le sol
dans un endroit ensoleillé. Son ombre portée est la plus courte à midi
locale.
Cercle indien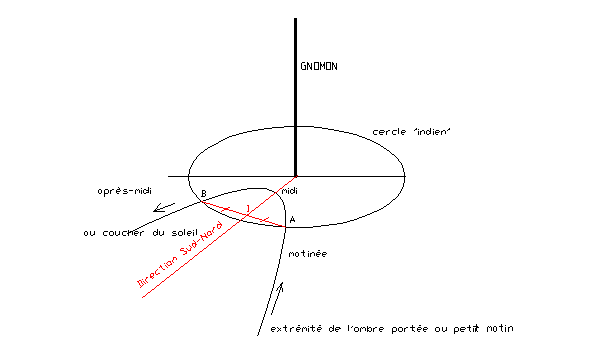
On trace
un cercle centré au pied du bâton (gnomon) de rayon suffisant pour que
l’ombre portée par l’extrémité du gnomon le coupe deux fois dans la journée :
le matin en A et le soir en B. On
joint le milieu I du segment AB au
pied du gnomon, on obtient ainsi la direction nord-sud du lieu.

I
- Les
instruments de visée
--------
Ce sont les appareils
qui servent à tracer les alignements et les angles.
Comparaisons
Sur le papier
Sur le terrain
Règle
Cordeau
Equerre
Groma ou l’équerre d’arpenteur
Compas
Cordeau
« Le principe de l’arpentage réside dans la
pratique de l’alignement » (Frontin)
1 -
Le Ferramentum dit
groma
C’est par excellence l’outil du limitatif. Celui qui l’utilise est
le gromaticus (Pseudo-Hygin).
Origine du mot –
« Le mot latin dérive lui-même
du grec gnomon, l’équerre, mais le mot révèle une transformation du gn-
en gr-conforme aux lois de la phonétique étrusque. Le Corpus
veteres ne donne jamais de description de la groma et ne
l’évoque que très rarement sous ce vocable, lui préférant son
synonyme de ferramentum, « l’instrument en fer » » (Chouquer-Favory)
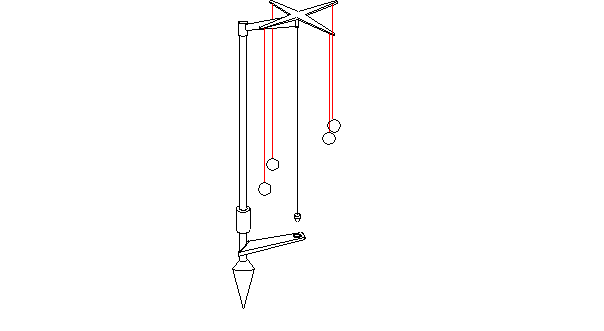 
La groma selon
Anne Roth-Congès
(Actes du Colloque de St-Etienne – p. 113).
2 - Les
dioptres –
Nom générique des appareils de visée. Elles
rassemblent la presque totalité des appareils à pinnules (viseurs) :
niveaux à eau, chorobate (vu par Newton),
etc.
Noter le genre
féminin du mot, à l’inverse du dioptre optique qui est la surface matérielle
qui sépare deux milieux de transparences différentes (surface d’une loupe,
plan d’eau, etc.)
3-
Les équerres d’arpenteur
Ce sont des chambres noires cylindriques ou prismatiques ou sphériques percées
de fentes verticales diamétralement opposées. Le montage le pus simple, celui
que nous présentons, est formé de quatre fentes,
disposées selon deux directions perpendiculaires.
On en connaît deux :
- Une exposée
au musée de Coblence, disparue depuis la dernière guerre,
-
L’autre, découverte il y a quelques années, par l’équipe d’Hervé
Petitot, au cours d’une fouille archéologique préventive, réalisée sur le
tracé de la future autoroute A29, commune d’Ennemain, dans la Somme, au
lieu-dit « l’Orme ». Elle est actuellement déposée au Service régional
de l’Archéologie de Picardie, 5, rue Daussy, 80 000 Amiens.
Ses caractéristiques :
Datation
au plus tard du dernier tiers du III e siècle ap. J.-C.
En
bronze, à forte teneur en plomb
Masse
: 814
g
Fondue en une seule pièce selon
la technique de la cire perdue
Longueur
(hors tout) :
18,5 mm (10 doigts)
Diamètre
: 76,5 mm
Largeur
des fentes
:
0,6 mm
Porte
16 fentes (angles 25 grades)
Etendue couverte à 50 m :
40 cm
(précision assez grossière de l’ordre de 0,8 %- Devait servir à
recomposer un parcellaire)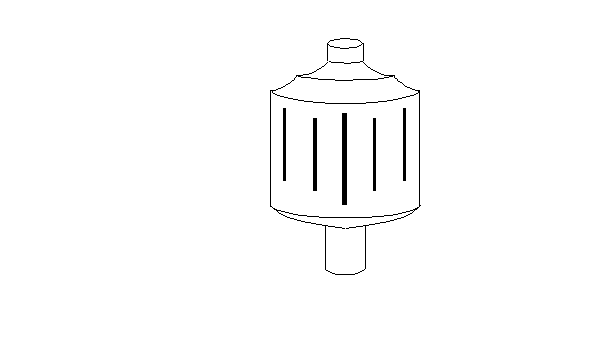

II
– Les instruments de nivellement
----
Le niveau d’eau
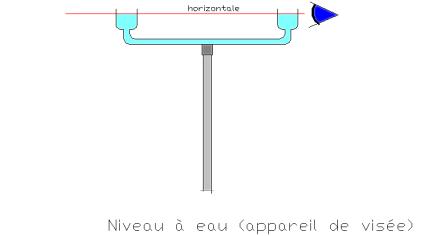
le chorobate
Description donnée
par Vitruve (livre VIII de "l'architecture"-
traduction de Louis Callebat - Les Belles Lettres- Paris - 1973).
.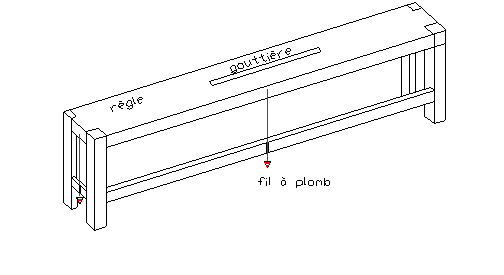
"… Le chorobate est une règle
longue d'environ 20 pieds (6
m). A ses extrémités cette règle a des pièces transversales parfaitement
identiques et assemblées en équerre aux bouts de la règle ; entre la règle
et ces pièces, fixées par des tenons, des traverses qui portent des lignes
exactement tracées en perpendiculaire, et, suspendus, un de chaque côté, à
la règle, des fils à plomb qui, lorsque la règle est en place, s'appliqueront
d'une manière rigoureusement identique aux lignes tracées, indiquant que la
position est horizontale.
Mais si le vent vient troubler l'opération
et, en les agitant, empêche les lignes de donner une indication précise, alors
on doit avoir sur la partie supérieure de l'instrument une gouttière longue de
5 pieds (1,5 m), large d'un doigt (1,8 cm), profonde
d'un doigt et demi (2,7 cm), y verser de l'eau, et, si l'eau touche
uniformément les bords supérieurs de la gouttière, on saura que l'on est de
niveau" .
Vitruve
ne précisant pas le mode d’emploi du chorobate, les uns lui associent deux
pinnules (viseurs) et le considèrent comme un instrument de visée, les autres
voient en lui un instrument de nivellement, comme les perches de frontin, en
somme.
Quelle
que soit la façon de l’employer, le chorobate reste un instrument trop imprécis
(1 cm pour 10 m) pour régler, avec la rigueur nécessaire, la pente de la
plupart des aqueducs. [Cf : communication
de Claude Larnac et
L’arpentage romain de
Gérard Chouquer et François Favory, p. 70]

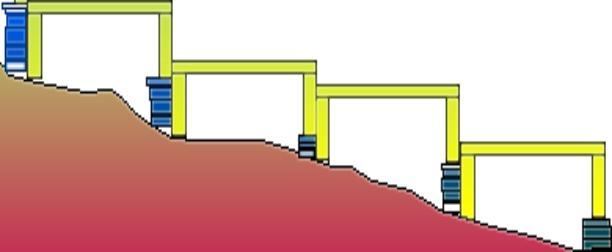
Autre
hypothèse d’utilisation du chorobate
Instrument de nivellement, on l’utilise sans pinnules, en le déplaçant de sa
longueur sur tout le tracé d’un aqueduc. (Théorie de Germain de Montauzan,
spécialiste des aqueducs de Lyon).
La dénivelée
sur un tracé serait la somme algébrique des indications données par les cales
étalonnées. Il est difficile d’imaginer la fiabilité de cet appareil
pour la construction d’un aqueduc, à travers bois et garrigue, sur une
cinquantaine de kilomètres, entre Uzès et Nîmes.
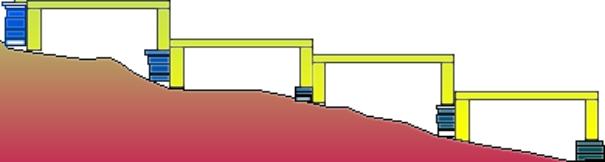 La
libra aquaria (pour mémoire) La
libra aquaria (pour mémoire)
La
dioptre d’Héron d’Alexandrie
----
C’est l’ancêtre du théodolite, mais ne possède pas d’optique.
Instrument
de nivellement, d’arpentage, d’astronomie.

L’importance
d’une horizontale de référence
-----
C’est à
partir du tracé de l’horizontale qu’on définit la pente d’un aqueduc, la
profondeur d’un tunnel. D’où l’intérêt qu’on porte à son degré
de précision.
.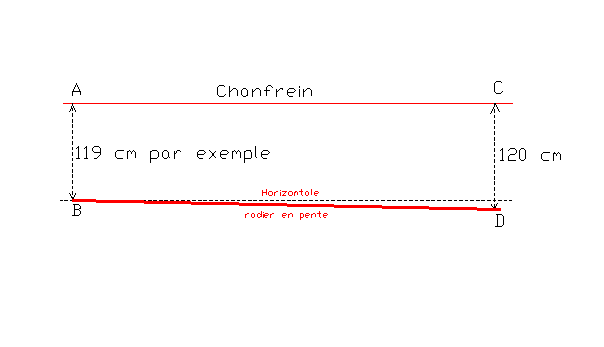
C’est à partir du tracé de l’horizontale
qu’on peut donner au radier une dénivelée de 1 cm par exemple sur sa
longueur. Il suffit pour cela de porter 1 cm de plus en C qu’en A.
Pour l’aqueduc de Nîmes, dont la pente moyenne est
de 25 cm par kilomètre, soit 1 cm pour 40 m, il suffit, si AC = 40 m, de porter
AB = 119 cm et CD = 120 cm.
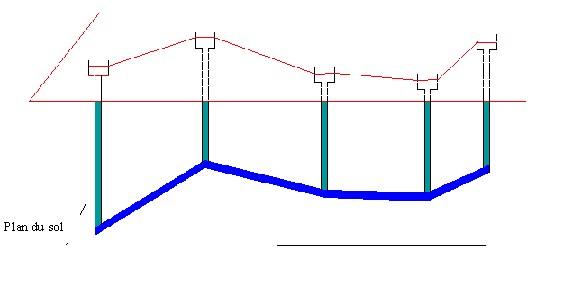
Encore
faut-il que la droite (AC) soit parfaitement horizontale, ou que l’imprécision
sur son horizontalité ne dépasse pas quelques millimètres sur 40 m. Seul, à
notre avis, le niveau à eau (type vases communicants) satisfait cette exigence
.

III
- Les
instruments de mesure et de dessin
----
La boutique de Vérus à Pompéï a livré d’autres objets :
une règle pliante, longue d’un pied romain avec une seule articulation. On en
voit d’autres au musée de Naples,
Deux compas en bronze
Des pinces, longues de 9 cm,
Un embout conique, long de 6,2
cm, d’usage incertain
Un cône de bronze, long de 14 cm,
Seize outils en fer, longs et minces,
Un style en bronze et un racloir en fer, pour écrire
sur une tablette de cire et l’effacer,
Un encrier et un canif, treize embouts cylindriques
en bronze (pour coiffer les jalons ou les perches (perticae)

Les
mesures de longueurs romaines
----
L’unité
principale est le pied (pes, au pluriel pedes )
Les
mesures de longueur romaines (pied = 29,57 cm)
extrait du tableau p. 73, Chouquer et Favory
|
Dénomination
latine
|
Traduction
|
Doigts
|
Pieds
|
Longueur
en cm ou m
|
|
Digitus
|
Doigt
|
1
|
1/16
|
18,5
cm
|
|
Palma
|
Paume
|
4
|
¼
|
73,9 cm
|
|
Pes
|
Pied
|
16
|
1
|
29,57 cm
|
|
Cubitus
|
Coudée
|
24
|
1,5
|
44,35 cm
|
|
Gradus
|
Grade, demi-pas
|
|
2,5
|
73,92 cm
|
|
Passus
|
Pas
|
|
5
|
1,4785 m
|
|
Decempeda
|
Perche, double pas
|
|
10
|
2,957 m (10 pieds)
|
|
Actus
|
|
|
120
|
35,48 m
|
|
Stadium
|
Stade
|
|
625
|
184,81 m
|
|
Milliarum
|
Mille
|
|
5000
|
1478,5 m
|

IV
- L’art
de la
mesure
----
1 - techniques
et principes du levé topographique
(Mme Anne Roth-Congès – Actes du
colloque de Saint-Etienne – p. 109)
L’outillage
La groma
-
La mise à la verticale : opération indispensable. (fils à plomb)
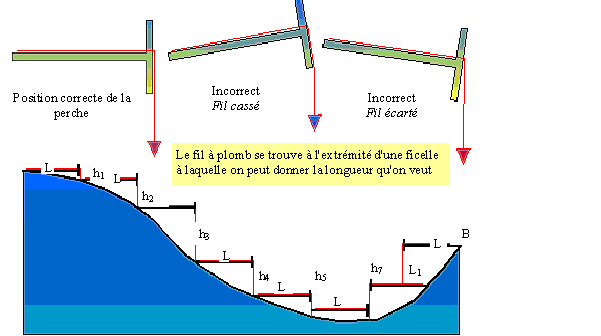
Les
perches de Frontin
-
Pour la mise à l’horizontale ou cultellation.
Les jalons -
pour les alignements
Le cordeau
Perches -
Pour mesurer les courtes distances sur le terrain (de l’ordre du pas)
L’hodomètre -
Pour mesurer les grandes distances (ancêtre du compteur kilométrique)

Tracé
des perpendiculaires
----
Balbus propose trois méthodes pour tracer une perpendiculaire :
1.
Les cercles sécants
Pour tracer la perpendiculaire en C à la droite
(AB), on prend sur une droite (AB) deux points équidistants de C à partir
desquels, on dessine deux cercles, centrés sur ces points et de même rayon.
Leur droite d’intersection est perpendiculaire à la droite (AB).
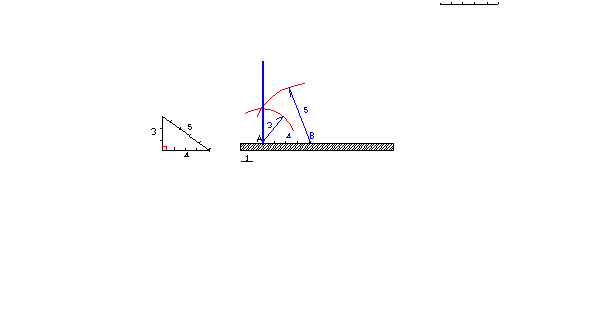
2. Triangle
inscrit dans un demi-cercle
Tout
triangle inscrit dans un demi-cercle est rectangle. Le diamètre du demi-cercle
en est l’hypoténuse (figure en bas, gauche).
Pour mener la perpendiculaire en A au
mur hachuré, il suffit de prendre un point B arbitraire, de tracer un cercle de
centre B qui coupe le mur en A et en un autre point C. La droite (CB) recoupe le
cercle en C’. (AC’) est la droite cherchée, perpendiculaire en A à (AC).
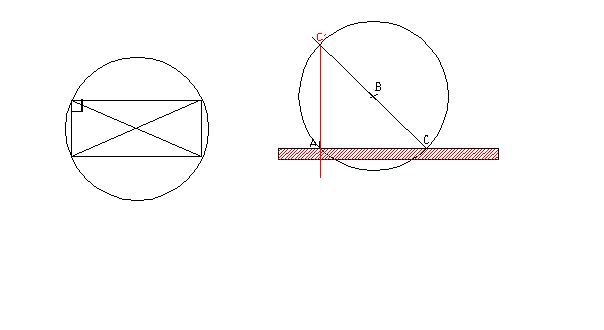
3 - Par le triangle de côtés 3,4,5 ou des multiples de 3,4,5.
(6,8,10 ou 9,12,15, etc.)
C’est un
cas particulier de la propriété de Pythagore, puisque
3² + 4² = 5². On peut le réaliser de plusieurs façons :

Procédé
du cordeau
Ce procédé est employé, encore de nos jours, par les maçons. Pour tracer la
perpendiculaire à partir du point A au mur :
1) -
On porte AB = 4 unités (mètre par exemple) le long du mur.
2)
- Le point C devant se trouver à 3
unités de A et à 5 de B, on trace deux arcs de cercle à l’aide d’un
cordeau : l’un de centre A et de rayon 3, l’autre de centre B et de
rayon 5. Le point C se trouve à leur intersection.
La perpendiculaire cherchée est la
droite (AC), bleue
sur le dessin.
Inconvénient : Selon les tensions exercées
sur le cordeau, il peut s’ensuivre une légère imprécision sur
l’intersection C.

La
corde à treize noeuds
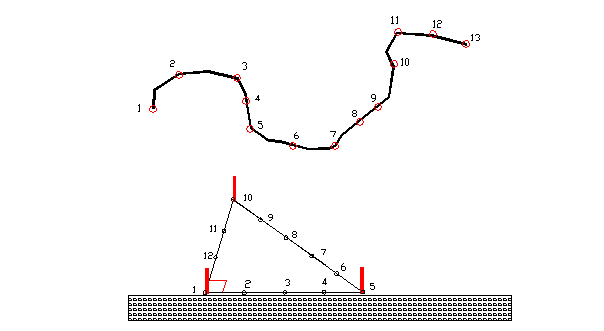
Principe
Treize
nœuds équidistants sont répartis sur une corde fine. Ils déterminent 12
intervalles égaux. Or 12 = 3 + 4 +
5. On reconnaît les trois nombres consécutifs qui permettent de construire un
triangle rectangle.
Méthode
Pour
élever à partir de A, la direction perpendiculaire au mur :
1)
on superpose en A les nœuds 1 et 13,
2)
puis on tend la corde à partir des nœuds 5 et 10, de manière que le nœud
5 soit contre le mur.
3)
Le triangle obtenu ayant pour côtés 3,4,5, il est évidemment
rectangle.
Le côté
[1 -10],
est donc perpendiculaire au mur en A.
Ce procédé, proche du précédent (cordeau), présente un avantage sur ce
dernier : Si l’on exerce une tension sur la corde, elle se répartit tout
au long di fil et n’altère pas la précision.
Une difficulté toutefois : Il
n’est pas aisé de bien disposer
les nœuds !
Ce procédé était connu des Grecs, avant l’époque romaine.

----
I
- La « varation » d’un fleuve
-
Opération par laquelle on mesure la largeur d’un cours d’eau, sans
mesure au sol. (Iunius Nypsius)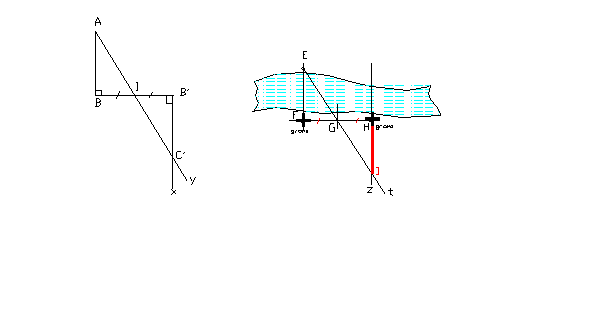
Principe (figure en haut, à gauche)
Je
pars du triangle rectangle ABI.
Je porte,
dans le prolongement de BI, la longueur IB’ = IB.
A partir de B’, je trace (B’x) perpendiculaire à
(BB’), qui coupe (AI) en C’.
Les
triangles rectangles ABI et C’B’I sont égaux et B’C’=AB
Si AB est la largeur du cours d’eau à mesurer, je peux, sans me mouiller,
mesurer [B’C’] qui est égal à [AB], la largeur du cours d’eau.
Sur
le terrain :
Pour connaître la largeur de la rivière :
1)
Je plante un jalon E verticalement sur le bord même ou à une distance
que je peux mesure (à condition d’avoir franchi la rivière à gué, à un
endroit convenable, ou à l’aide d’un pont),
2)
Je place la groma ou l’équerre d’arpenteur en F sur
l’autre rive,
3)
Je repère la direction (FH) perpendiculaire à (EF) que je matérialise
avec un cordeau
4)
Sur cette direction je me donne un point G arbitraire, à partir duquel
je porte GH = FG.
5)
Je repère la direction (Gt) que je matérialise avec un cordeau et la
direction (Hz) perpendiculaire à (FH). Leur intersection I,
me donne HI = EF, la largeur de la rivière.
II
-
Relier par une droite deux points non visibles l’un depuis l’autre

(Héron. Rapporté
par Anne Roth-Congès – p. 128)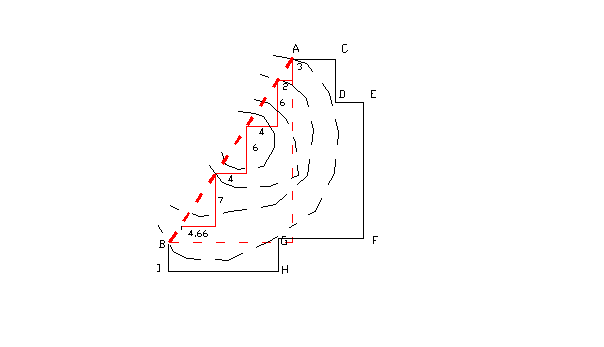
A l'aide de la groma ou d’une équerre d’arpenteur, on parcourt le tracé le
plus adapté de A jusqu’à B. Ce parcourt repéré :
1) on fait la somme des abscisses positives ou négatives
AC + DE – FG - HI
2) puis des ordonnées
CD + EF + GH -IB,
3)
On les compare.
Dans
l’exemple ci-dessus, on obtient le rapport 3/2
A partir de A, il suffit alors de progresser verticalement de 3 et de reculer
horizontalement de 2, puis de 6 et reculer de 4, etc.
Dans la pratique, deux équipes fonctionnent (tunnel d’Eupalinos, à
Samos, par exemple – V e siècle av. J.-C.), l’une à partir de
A, l’autre à partir de B. le principe restant le même.
La droite (AB) est la droite cherchée

III
- Calculer
la hauteur d’un point dont la base
est accessible
----
Plusieurs méthodes, basées sur les propriétés développées par le
mathématicien et savant grec Euclide (365 ? – 276 ? av. J.-C.),
attribuées 19 siècles plus tard au philosophe, moraliste, physicien René
Descartes (1596 – 1650 ap. J.-C.).
1) Superposition des ombres
portées (proposition XVIII de l’Optique
d’Euclide)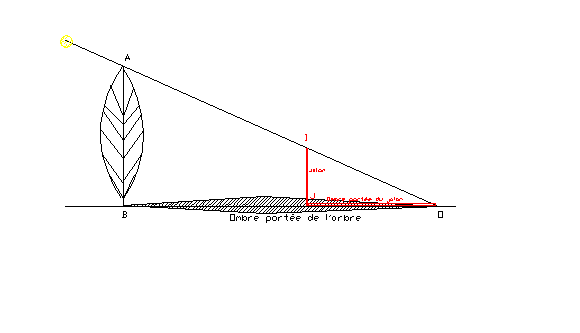
On place un jalon sur l’axe de l’ombre portée de l’arbre, par exemple, de
telle manière que l’extrémité de l’ombre portée de l’arbre et celle du
jalon coïncident.
Sans calculs (Ecoles primaires)
Sur
une feuille de dessin on reproduit, à raison de 1 cm pour 1 m (ou autres
valeurs simples), les distances OB, OJ, IJ. En B on élève la perpendiculaire
qui coupe OI en A On esure AB sur la feuille, on en déduit AB sur le terrain.
A l’aide d’un calcul simple (A partir classe de quatrième).
Les
triangles rectangles OBA et OJI sont semblables. On déduit :
AB/IJ = OB/OI. D’où AB = (IJ/OI) x OB.
Compte tenu que OB, OJ et
IJ sont faciles à mesurer, le calcul de AB est simple.
Exemple : OB = 8 m, OI = 1,5 m, IJ = 2m.
Dans ce cas AB = (2 : 1,5) x 8 = 10,7 m.
Retenons que AB = (IJ/OI)
x OB. Le rapport IJ/OI porte
le nom de tangente de l’angle aigu IOJ. La
trigonométrie faisait ses premiers pas avec Ptolémée (101-179 ap. J.-C.) et
fut d’un maniement plus facile avec Aryabhata, mathématicien astronome
indien, inventeur de la règle de trois, découvreur de la cause des éclipses
de soleil et de lune, qui introduit le calcul du sinus en trigonométrie
en 527. Toutefois, bien avant lui, et sans lui donner de nom, on savait
probablement mettre en évidence le rapport (IJ/OI),
dénommé plus tard, tangente de l’angle
aigu.
Ces
deux méthodes peuvent s’utiliser en l’absence de soleil, si l’on ne
recule pas devant la situation inconfortable qui consiste à mettre l’oeil au
niveau di sol. A moins qu’on contourne la difficulté ….

2 - Méthode
du miroir (d’Euclide – proposition XIX de l’Optique)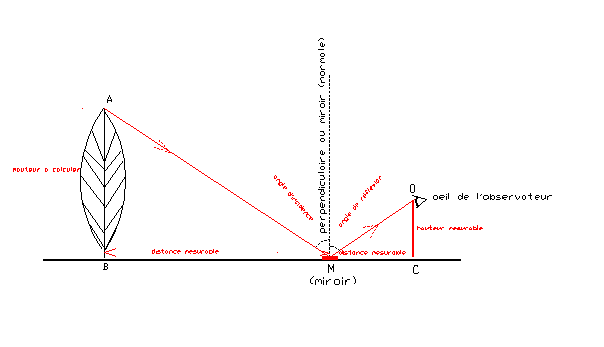
Méthode
rappelée par Catherine Jacquemard (colloque de St-Etienne)
Principe : Loi de la réflexion
(égalité des angles d’incidence et de réflexion) de la lumière dites de
Descartes (XVII e ap. J.-C.), mais énoncée en partie par Euclide
(Proposition XIX Traité sur l’Optique ).
Les triangles [MBA] et [MCO]
sont semblables. Il s’ensuit que AB = (OC/MC)
x MB.
OC, MC et MB étant
directement mesurables, la calcul de AB ne présente aucune difficulté.
On pourrait encore reproduire par un dessin, à l’échelle, le schéma
ci-dessus et procéder par mesure, sur le papier, sans effectuer le moindre
calcul.

IV - Calculer
la hauteur d’un point dont la base
n’est pas accessible
----
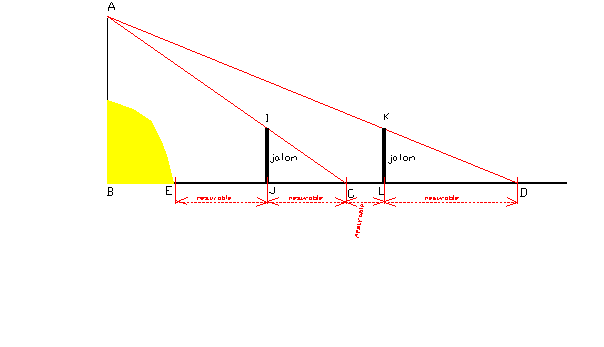
En s’appuyant sur les paragraphes précédents :
1
- On
peut procéder par des dessins (aucun calcul)
2 -
On peut calculer (programme de quatrième)
AB = (IJ/JC) x (JE + BE)
(Mais BE est inconnu)
AB
= (KL/LD) x (DE + BE)
(BE toujours inconnu).
Prenons un exemple :
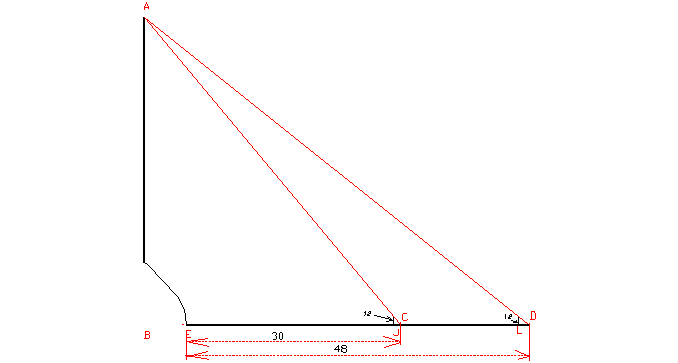
IJ = KL
= 1,2 m
JC
= 1 m et EJ = 29 m
donc AB
= (IJ/JC) x
CB = (1,2 : 1) x (30 + EB)
AB = 1,2 x (30 + EB)
(égalité1)
On
recule le jalon de 17,5 m. On mesure LD = 1,5 m.
AB
= ( KL/LD) x
DB = (1,2 : 1,5) x (1,5 + 16,5 + 1 +29 + EB)
AB = 0,8 x (48 + EB)
(égalité 2)
Rapprochons les égalités (1) et (2) qui donnent toutes deux une expression de
AB. On
a : 1,2
x (30 + EB) = 0,8 x (48+EB)
36
+ 1,2 EB = 38,4 + 0,8 EB
1,2
EB – 0,8 EB = 38,4 – 36
0,4 EB = 2,4
EB
= 6
Si l’on porte la valeur EB = 6 dans l’une
ou l’autre des égalités (1) ou (2), on trouve AB = 43,2 m
*
*
Il serait possible de compliquer les situations, mais tel n’est pas notre but.
On pourrait chaque fois, se ramener aux cas abordés ci-dessus.
 Retour sommaire
Retour haut de page
Retour sommaire
Retour haut de page  Suite :Visite
Suite :Visite 
|